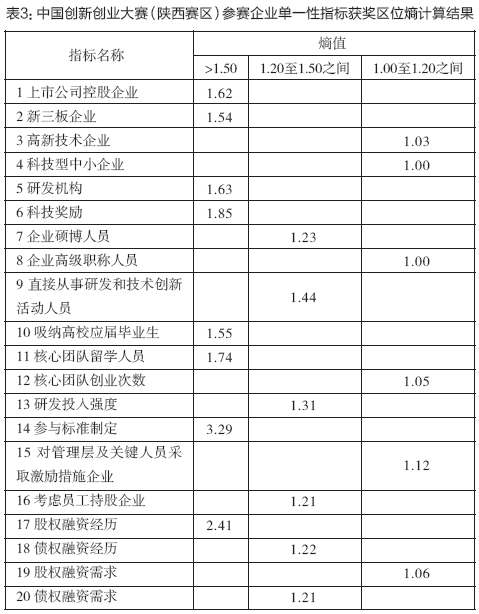表3：中国创新创业大赛（陕西赛区）参赛企业单一性指标获奖区位熵计算结果

业群体相对于参赛企业总体所具有的优势，即对应于一般的区位熵理论，本研究的背景区域为参赛企业总体，若干区域仅固定为获奖企业群体一类，以区位熵值进行获奖企业特征的分析。
　　（1）单一性指标的计算公式与内涵解释
　　基于前述的单一性指标的意义，替换公式（1），得单一性指标的计算公式：
　　其中，i为企业的特性指标序号，i=1上市公司控股企业，2新三板企业，……，20债权融资需求，即对应着单一性指标；e为获奖企业数值，E为参赛企业数值。如q₁即为第1项特性指标——上市公司控股企业获奖区位熵。因为获奖企业群体应该是参赛企业总体中比较优质的部分，所以可以估计的是：计算所得的q_i应该都是大于或等于1的数值；从20个单一性指标中寻求与企业获奖最相关的若干突出性指标，即从q₁，q₂，……，q₂₀中得出的若干极大值指标，就对应着企业获奖实力的重要属性。
　　（2）结构性指标的计算公式与内涵解释
　　基于前述的结构性指标的意义，替换公式（1），得结构性指标的计算公式：
　　其中，i仍为企业的特性指标序号，i=21行业，22组别，……，29三项专利，即对应着结构性指标；每一项结构性指标内含的若干种表现，用j表示；e为获奖企业数值，E为参赛企业数值；如q₂₁，6即为第21项特征指标——行业中内含的第6种表现——新能源汽车行业获奖企业的区位熵。
　　当q_ij>1时，表明具有第j种表现的i特性的企业有更明显的获奖优势；当q_ij=1时，表明具有第j种表现的i特性的企业没有获奖优势、也没有获奖劣势；当q_ij<1时，表明具有第j种表现的i特性的企业有获奖劣势。与单一性指标不同，研究结构性指标是从第i项结构性指标的若干种表现中，寻求与参赛企业获奖可能性相关的某突出性表现，即从q_i1，q_i2，……，q_ij，……中得出大于1的值，大于1的q_ij所对应的i特性下具有第j种表现的企业，则更具获奖的可能性。
　　（二）获奖区位熵模型的应用
　　1、数据的选取
　　由于2017年以前，参赛企业不分初创组和成长组，而且若干数据未完整统计，且2020年起行业分布从六个行业调整为七个行业，所以为选取最新数据并保持数据在行业及组别等分类上的一致性，本研究选用中国创新创业大赛（陕西赛区）2020年以来的参赛及获奖企业数据，而且为避免某一年份数据值的偶然性，数据采用2020-2023年的连续合计数据进行测算。
　　2、企业获奖区位熵测算结果及其分析
　　（1）单一性指标的获奖区位熵测算结果及其分析
　　如表3所示，以上20项单一性指标的获奖区位熵均大于或等于1，表明获奖企业确实是参赛企业中的优质群体。
　　其中，1上市公司控股企业、2新三板企业、5研发机构、6科技奖励、10吸纳高校应届毕业生、11核心团队留学人员、14参与标准制定、17股权融资经历等八项指标的获奖区位熵明显大于1，均在1.5以上，表明这八项指标对应的企业特性与企业获奖实力高度正相关，特别是14参与标准制定和17股权融资经历指标的熵值属20项指标中的两个极大值，即3.29和2.41，表明这两项指标对应的是获奖企业所具有的特别突出的性质。
　　7企业硕博人员、9直接从事研发和技术创新活动人员、13研发投入强度、16考虑员工持股企业、18债权融资经历、20债权融资需求等六项指标的获奖区位熵在1.2与1.5之间，表明这六项指标对应的企业特性与企业获奖实力也正相关，但与上述八项指标相比稍逊色一些。