识，更重要的是数学思想方法。转化法是从具体的事物中抽象出数学元素，也是小学数学学习中分析问题和解决问题的一种重要的数学思想。
　　比如这道题，“有78颗糖果，按小军、小芳、敏敏、小雪的顺序，每人分2颗，谁分到最后一颗糖果？”初次见到这道练习题，学生们像炸开了锅似的，毫无头绪，不一会儿有的同学就想到了办法。“按小军、小芳、敏敏、小雪的顺序，每人分2颗”可以转化为“小军、小军、小芳、小芳、敏敏、敏敏、小雪、小雪”8个为一组规律。
　　此题实际就是8颗珠子为一组，第78颗珠子是什么颜色的？把不会的转化为会的，去除语言形式的抽象外壳，抓住数量关系的本质来解题，会一道题也就会一类题了。
　　（三）循序渐进，通过题组的形式来学习
　　一年级习题中曾经有过这样一道思维拓展类题目：小方送给小红6本书后，两人书的本数一样多，原来小方比小红多几本？学生们往往看到题后容易蒙了，老师们看到题后往往容易懊恼！这是为什么呢？讲过、练过、还会错过！
　　新阶段的学习从易到难，拾级而上，层层递进，效果不错。
　　（1）8的一半是多少？即把8分成相同的两部分4和4，4就是8的一半。
　　（2）小方有15本书，小红有9本书。小方和小红相差几本书？
　　（3）小方有15本书，小红有9本书。小方给小红几本书后，两人的同样多？
　　（4）小方送给小红6本书后，两人书的本数一样多，原来小方比小红多几本？
　　（5）小方和小红的铅笔一样多，如果小方把自己的铅笔给小红6支，这时小方比小红少几支？
　　火候不到，独立的学习容易形成思维定式，就会学习的那种；所以先单个学习，再成组对比学习。对比学习、变式学习，掌握本质，将知识学活。
　　（四）数形结合，通过画图法学习
　　数形结合是一种利用几何图形来解决数学问题的方法，它通过将数学概念与空间图形相结合，帮助学生更直观地理解和解决问题。在解题过程中，画图法可以显著提升解题的效率和准确性。
　　例如同一道题，15名小朋友排队，班长排在第7个，教练发令：“向后转”。这时，班长排在第几个？从形象到抽象，有不同的解题方法。
　　1、直观法解题
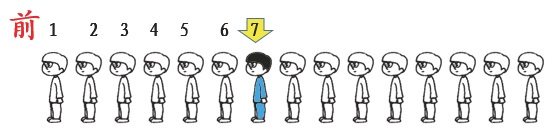
　　瞧！15名幼儿园小朋友排着队来了。最初假设他们是面向这一边列队站立的。面朝着的方向就是前面，“班长（穿蓝色衣服的）排在第7个”也就是说，此刻从前往后数，班长是第7个。
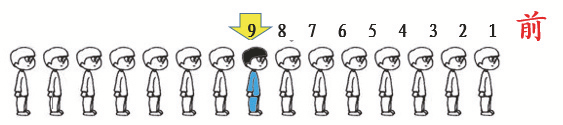
　　“向后转！”此刻面朝着的方向变了。从前往后数，班长排第几呢？画图后就可以清晰数出，班长排在第9个。
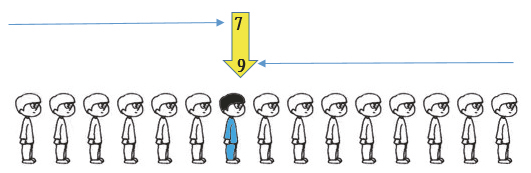
　　同一名班长一会儿排在第9个，一会儿又排在第7个，这是为什么呢？因为数法不同，所以得到的结果有可能不同。
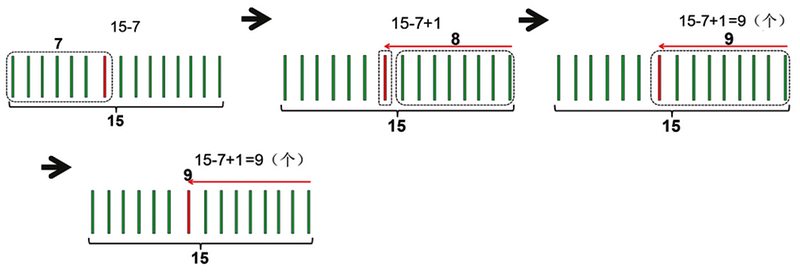
　　2、半直观法解题
　　还可以用15根小棒来表示小朋友，班长用不同颜色的小棒来区分。
　　3、抽象法解题
　　从总数“15”人里面去掉这一侧的“7”人，得到另一侧是“8”人，“8+1”就是“9”人，班长排第9个。
　　4、延伸解题方法
　　整个的学习过程试图体现从直观形象思维向抽象逻辑思维的过渡。而“小朋友图”与“小棒图”等直观形式为学生理解提供适当的“脚手架”。从头思考和由浅入深、由儿童粗糙的数学现实到数学王国的数学化过程。